CONSIDERACIONES INICIALES
- El reloj de sol sirve para cualquier inclinación y orientación pero ha de ser plano.
- Dispone de dos estiletes (gnomon)
- ESTILETE PERPENDICULAR, E0. Aguja recta perpendicular al plano del reloj de sol.
- ESTILETE POLAR, EP. Aguja apoyada sobre el plano y el extremo del estilete perpendicular apuntando al polo celeste, Norte o Sur según el hemisferio.
- Puntos y coordenadas
- ORIGEN DE COORDENADAS, O. Punto donde el estilete perpendicular se apoya en el plano, con dos ejes y sus coordenadas.
- EJE OX. Siempre horizontal. Su ABSCISA, x, se cuenta positiva hacia la derecha.
- EJE OY. En la dirección de máxima pendiente del reloj. Su ORDENADA, y, se cuenta positiva hacia arriba.
- CENTRO, I. Punto donde el estilete polar se apoya en el plano. Se localiza en las coordenadas ( x0 , y0 )
- ÁNGULO DE INCLINACIÓN DEL ESTILETE POLAR, ψ, con respecto al plano.
- PUNTO P. Extremo del estilete perpendicular.
- PUNTO P'. Extremo de la sombra del estilete perpendicular.
- Datos necesarios:
- LATITUD LOCAL, φ.
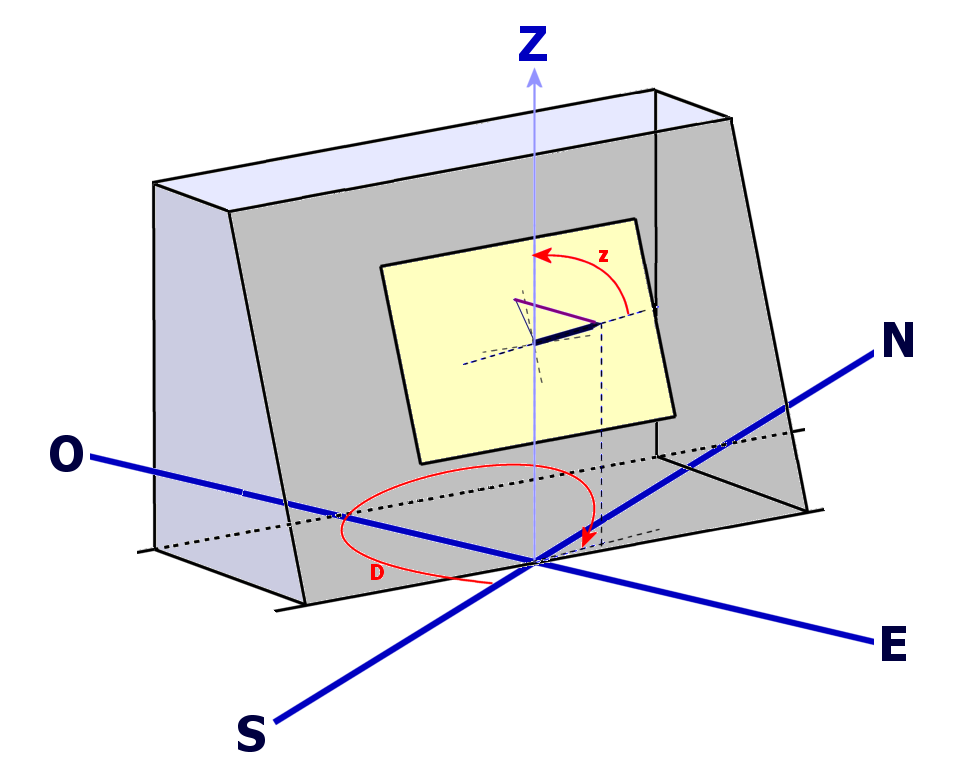
- DISTANCIA CENITAL, z de la dirección definida por el estilete perpendicular.
- Si z = 0º ⇒ El reloj es horizontal
- Si z = 90º ⇒ El reloj es vertical
- DECLINACIÓN GNÓMICA, D, acimut de la perpendicular al plano del reloj de sol, medido desde el meridiano sur hacia el oeste.
- Si D = 0º ⇒ E0 apunta al SUR
- Si D = 90º ⇒ E0 apunta al OESTE
- Si D = 180º ⇒ E0 apunta al NORTE
- Si D = 0º ⇒ E0 apunta al OESTE
- LONGITUD del estilete perpendicular, a.
- ÁNGULOS HORARIOS DEL SOL, Tabla H. Comenzando en valores negativos con incrementos constantes (5º o 15º, habitualmente) hasta alcanzar los mismos positivos
- DECLINACIONES SOLARES, Tabla δ. Con los valores correspondientes a las fechas en las que la Longitud del Sol es múltiplo de 30º, es decir; (-23,44º , -20,15º , -11,47º , 0º , +11,47º , +20,15º , +23,44º)
- Croquis general del reloj de sol
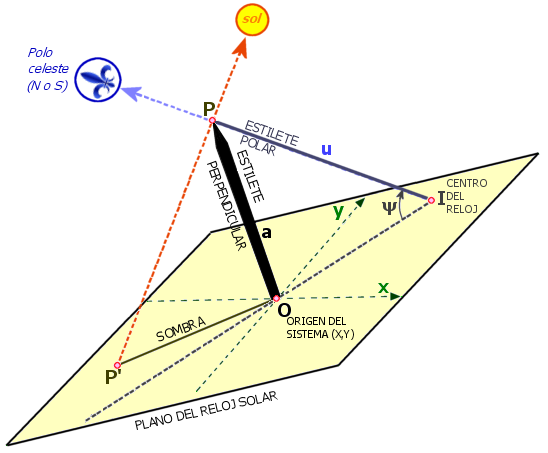
- ORIGEN DE COORDENADAS, O. Punto donde el estilete perpendicular se apoya en el plano, con dos ejes y sus coordenadas.
PARÁMETRO AUXILIAR
ARGUMENTOS
- Latitud del lugar, φ en grados
- Distancia cenital del estilete perpendicular, z en grados
- Distancia gnómica, D en grados
CÁLCULOS
(Devuelve el valor P)
VARIABLES BIDIMENSIONAL DE CONTROL
ACLARACIÓN
Se conforman para cada valor de la tabla H y de la tabla δ
ARGUMENTOS
- Latitud del lugar, φ en grados
- Distancia cenital del estilete perpendicular, z en grados
- Distancia gnómica, D en grados
- Tabla de ángulos horarios del Sol, H en grados
- Tabla de declinaciones, δ en grados
CÁLCULOS
- Para cada valor Hi y cada valor δj:
(Devuelve la tabla bidimensional Q)
AUXILIARES DE COORDENADAS
ACLARACIÓN
Se conforman para cada valor de la tabla H y de la tabla δ
ARGUMENTOS
- Latitud del lugar, φ en grados
- Distancia cenital del estilete perpendicular, z en grados
- Distancia gnómica, D en grados
- Tabla de ángulos horarios del Sol, H en grados
- Tabla de declinaciones, δ en grados
CÁLCULOS
- Para cada valor Hi y cada valor δj:
(Devuelve las tablas bidimensionales Nx y Ny)
COORDENADAS DE LAS SOMBRAS (DEL EXTREMO ESTILETE PERPENDICULAR)
ACLARACIÓN
Se conforman para cada valor de la tabla H y de la tabla δ
ARGUMENTOS
- Longitud del estilete perpendicular, a
- Tabla bidimensional variable de control, Q
- Tablas bidimensionales auxiliares de coordenadas, Nx y Ny
- Tabla de ángulos horarios del Sol, H en grados
- Tabla de declinaciones, δ en grados
CÁLCULOS
- Para cada valor Hi y cada valor δj:
(Devuelve las coordenadas de todas las sombras en tablas bidimensionales x e y )
LONGITUD DEL ESTILETE POLAR
ARGUMENTOS
- Longitud del estilete perpendicular, a
- Parámetro auxiliar, P
CÁLCULOS
(Devuelve la longitud u )