ESFERA CELESTE

La esfera celeste es una esfera imaginaria de radio arbitrario y centro en el observador, sobre la cual se proyectan las estrellas para estudiar sus posiciones relativas.

Movimiento diurno es el movimiento aparente de rotación de la esfera celeste, de levante a poniente, debido al movimiento real de rotación de la Tierra de poniente a levante. De él, por tanto, participan todos los cuerpos celestes.

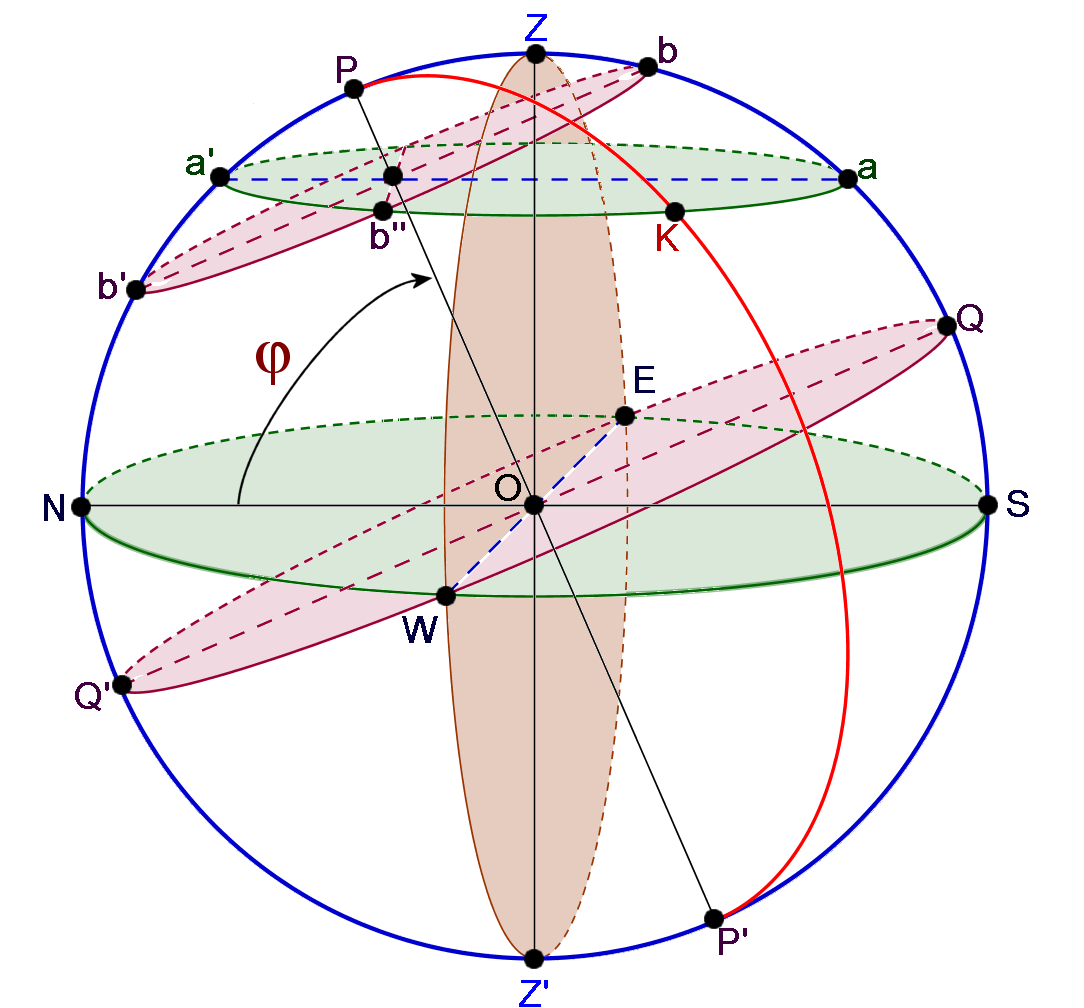
Eje del mundo es el diámetro alrededor del cual parece girar la esfera celeste. Su localización varia con el tiempo.

Polos celestes (P y P') son los puntos de intersección del eje del mundo con la esfera celeste. Son, por tanto, los únicos puntos del cielo que no participan del movimiento diurno. De éstos el que vemos desde nuestro lugar de observación (por hallarse sobre nuestro horizonte) es el polo norte P, y el diametralmente opuesto es el polo sur P'.

Vertical de un lugar (ZZ') es el diámetro de la esfera celeste dado por la dirección de la plomada. Su punto de intersección con la esfera celeste situado en el hemisferio visible para el observador se denomina cenit (Z). El situado en el hemisferio invisible se denomina nadir (Z').

Horizonte astronómico o verdadero es el plano diametral ortogonal a la vertical. La intersección de dicho plano con la esfera celeste es un círculo máximo denominado también horizonte. EL horizonte astronómico divide a la esfera celeste en dos hemisferios, situados por encima y por debajo del mismo, que se denominan hemisferio visible y hemisferio invisible respectivamente

Horizonte sensible o aparente es el círculo menor que se obtiene al situarnos a una cierta altitud sobre el nivel del mar y trazar un cono con vértice en el observador y generatrices tangentes a la superficie de la Tierra. El ángulo formado por una generatriz del cono y el horizonte verdadero se denomina depresión del horizonte.

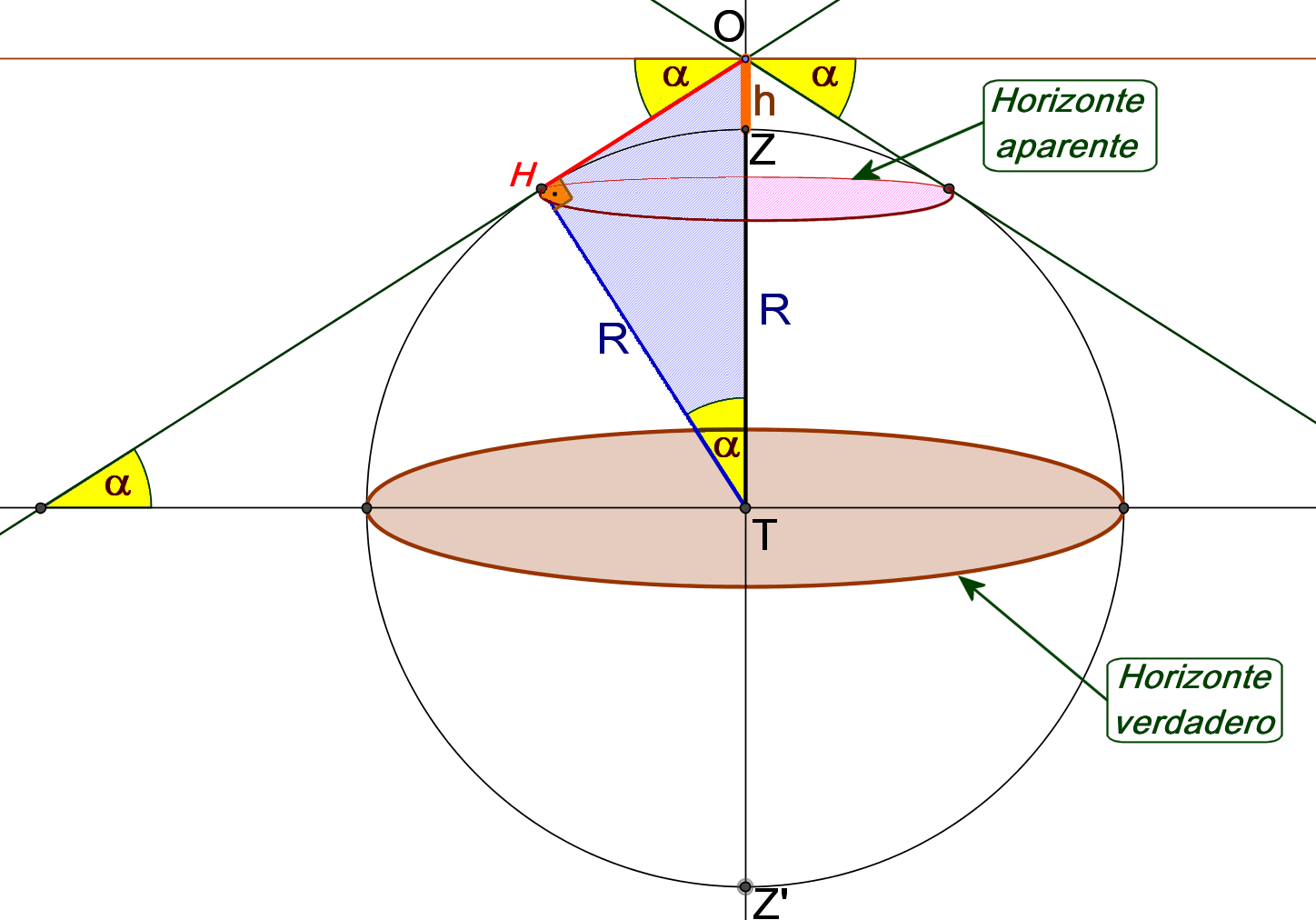
Aclaración

Consideremos un PUNTO DE OBSERVACIÓN, O situado sobre el punto Z a una altura h sobre el nivel del mar. Esta altura es despreciable con respecto a las dimensiones terrestres, y en particular con respecto al radio R.

El triángulo OTH es rectángulo en H, y pr tanto:

$cos\left(\alpha \right)=\frac{R}{h+R}$

Por otro lado, utilizando el seno del ángulo mitad y sustituyendo:

$sen\left(\frac{\alpha }{2}\right)=\pm \sqrt{\frac{1-cos\left(\alpha \right)}{2}}\iff 2·{sen}^2\left(\frac{\alpha }{2}\right)=1-cos\left(\alpha \right)=1-\frac{R}{h+R}=\frac{h}{h+R}$

Además, sabemos que:

$\underset{x\to 0}{\mathrm{Lim}}\left[\frac{sen\left(x\right)}{x}\right]=1$

es decir, cuando "x" es muy pequeña, en cociente tiende a 1 y en consecuencia, x ≅ sen(x) (se comportan de modo similar).

Así pues, como h es muy pequeña, "α/2" también será muy pequeña:

$2·{sen}^2\left(\frac{\alpha }{2}\right)=\frac{h}{h+R}\cong \frac{h}{R}\iff \frac{\alpha }{2}\cong sen\left(\frac{\alpha }{2}\right)=\sqrt{\frac{h}{2·R}}\iff \alpha =\sqrt{\frac{2·h}{R}}$

Ecuador celeste es el plano diametral ortogonal al eje del mundo o, también, el círculo máximo determinado por la intersección de dicho plano con la esfera celeste.

Plano meridiano es el plano diametral determinado por el eje del mundo y la vertical. Su intersección con la esfera celeste es el meridiano del lugar.

Meridiana es el diámetro determinado por la intersección del plano meridiano con el horizonte verdadero. Sus intersecciones con la esfera celeste constituyen los puntos cardinales norte N y sur S .

Latitud del lugar φ es el ángulo formado por la meridiana y el eje del mundo. Su complementario (Φ = 90°-φ) se denomina colatitud.

Perpendicular es el diámetro determinado por la intersección del ecuador celeste con el horizonte verdadero. Sus intersecciones con la esfera celeste constituyen los puntos cardinales este E y oeste W .

Primer vertical es el plano diametral determinado por la vertical y la perpendicular. También se denomina así el círculo máximo determinado por la intersección de dicho plano con la esfera celeste.

Línea del medio cielo es el diámetro determinado por la intersección del ecuador celeste con el plano meridiano. Su punto de intersección con la esfera celeste situado en el hemisferio visible se denomina medio cielo Q

Verticales son los planos que pasan por la vertical. Los círculos máximos intersección de dichos planos con la esfera celeste reciben también el nombre de verticales. Son verticales tanto el plano meridiano como el primer vertical.

Almicantarates son los círculos menores de la esfera celeste paralelos al horizonte.

Planos horarios son los planos diametrales que pasan por el eje del mundo.

Círculos horarios son los círculos máximos determinados por su intersección con la esfera celeste.

Paralelos celestes son los círculos menores de la esfera celeste paralelos al ecuador.

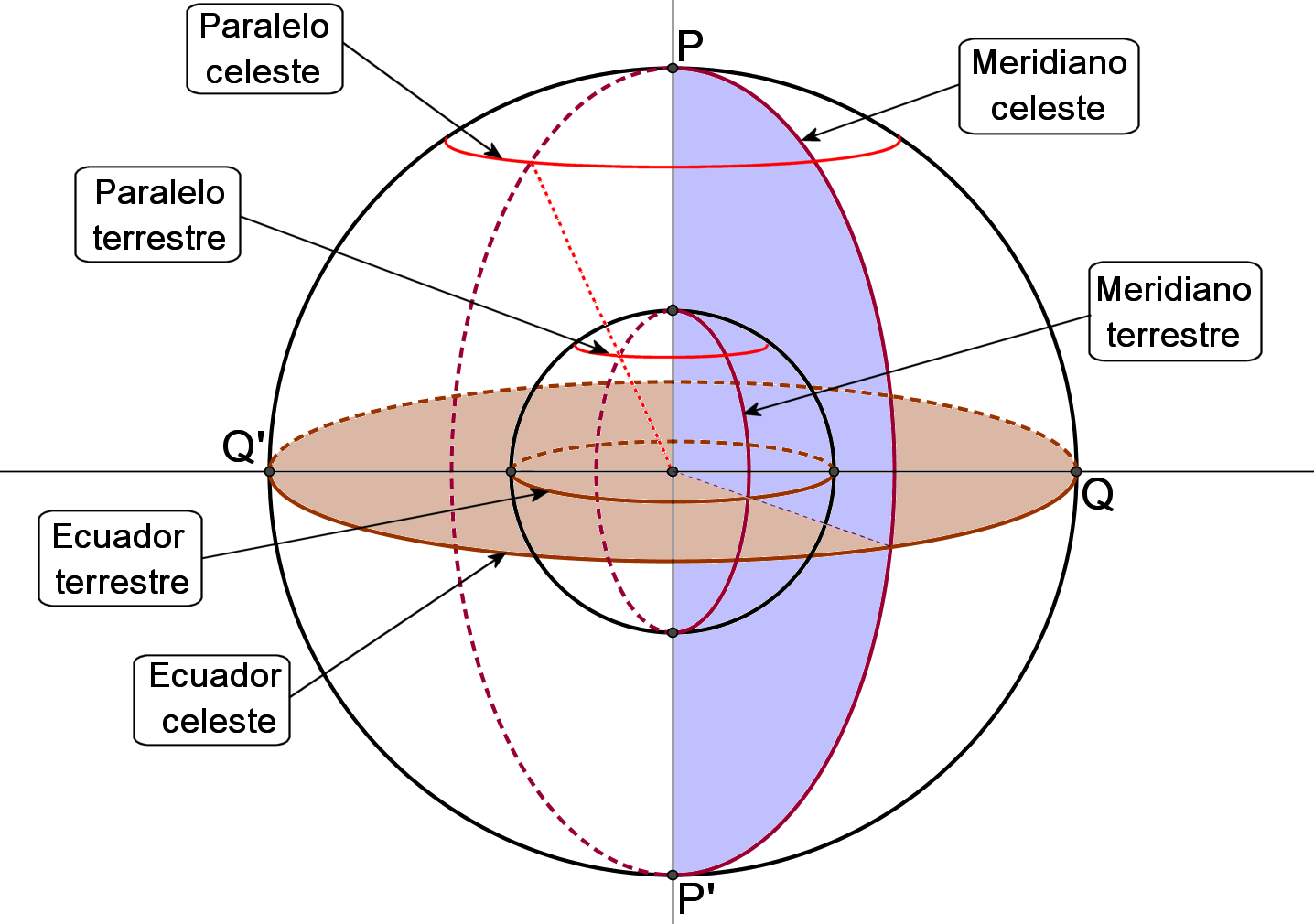
La línea de polos PP' divide al meridiano del lugar en dos semiplanos:

• el meridiano superior, que contiene al cenit
• el meridiano inferior, que contiene al nadir

Consideremos ahora un punto Z de la Tierra, y una estrella en el cielo. La rotación terrestre hace que parezca que la estrella describe un paralelo celeste girando 360º de ESTE a OESTE.

La estrella comenzará a ser visible en el punto 1, ORTO. Recorrerá el paralelo en sentido ESTE a OESTE hasta alcanzar el punto 2, CULMINACIÓN SUPERIOR. Seguirá su trayectoria hasta el punto 3, OCASO; llegará al punto 4, CULMINACIÓN INFERIOR hasta alcanzar de nuevo el punto 1.

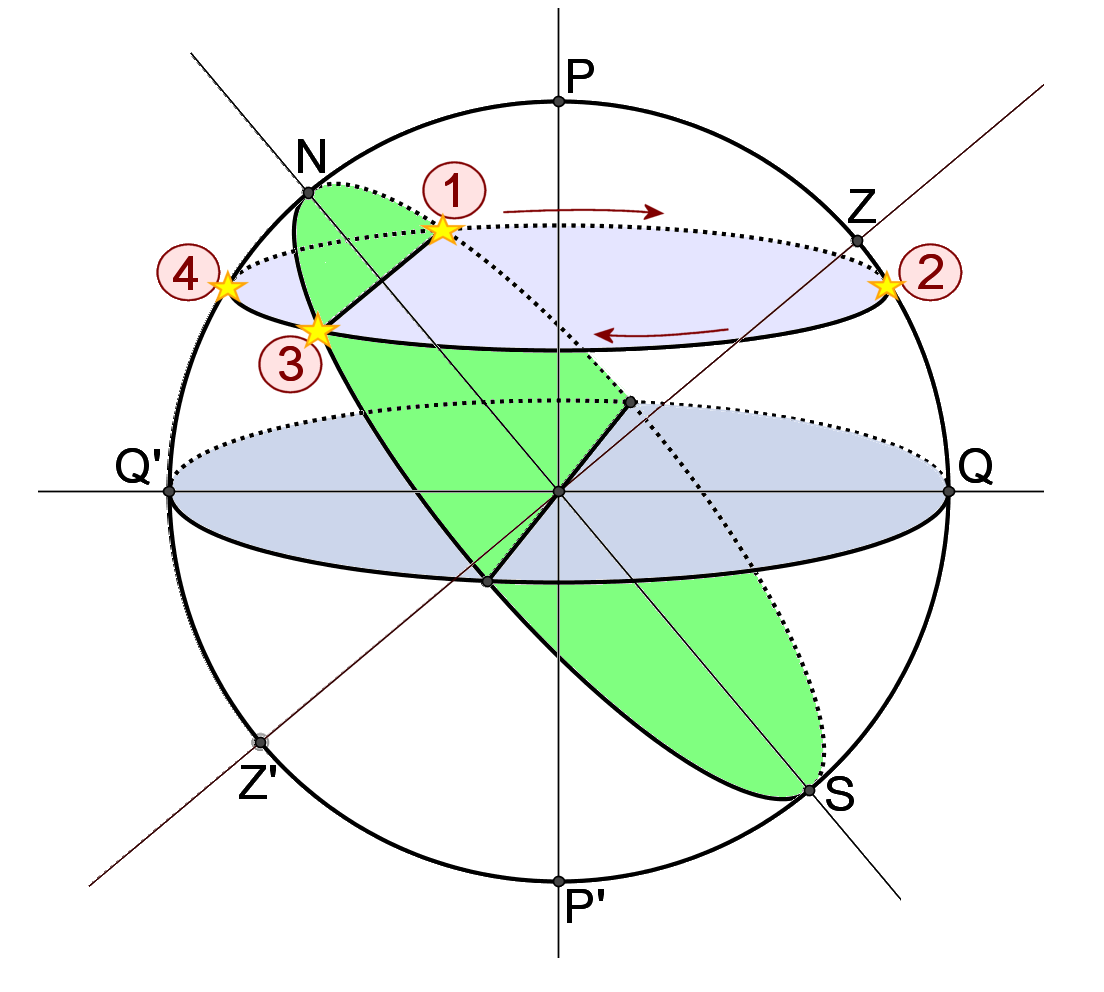
Fuente: Astronomía esférica y mecánica celeste (Orús-Catalá-Nuñez)

INICIO REGRESAR

CIRCULO HORARIO DE UN ASTRO

Círculo horario es el meridiano celeste que pasa por el astro.

INICIO REGRESAR

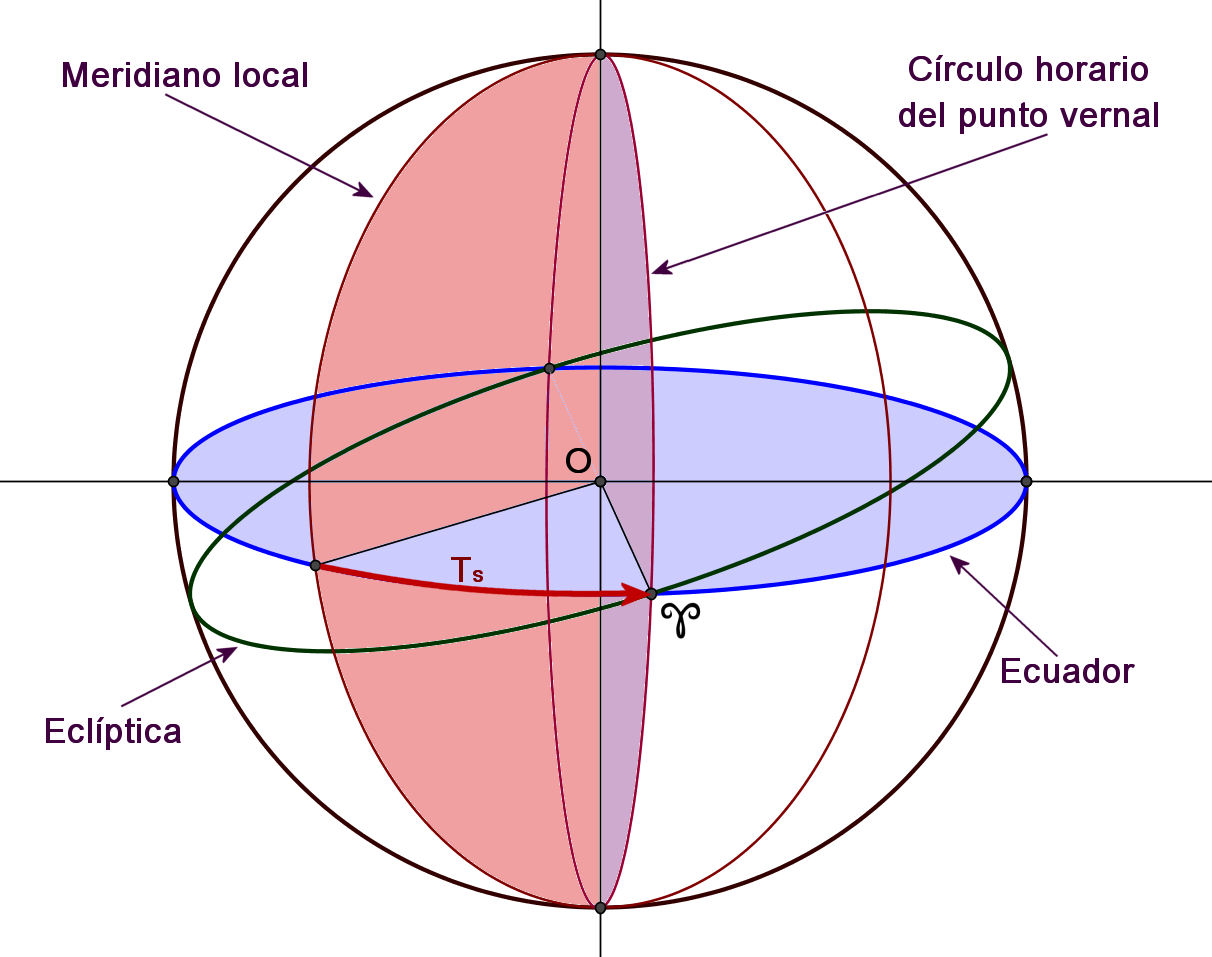
ÁNGULO HORARIO

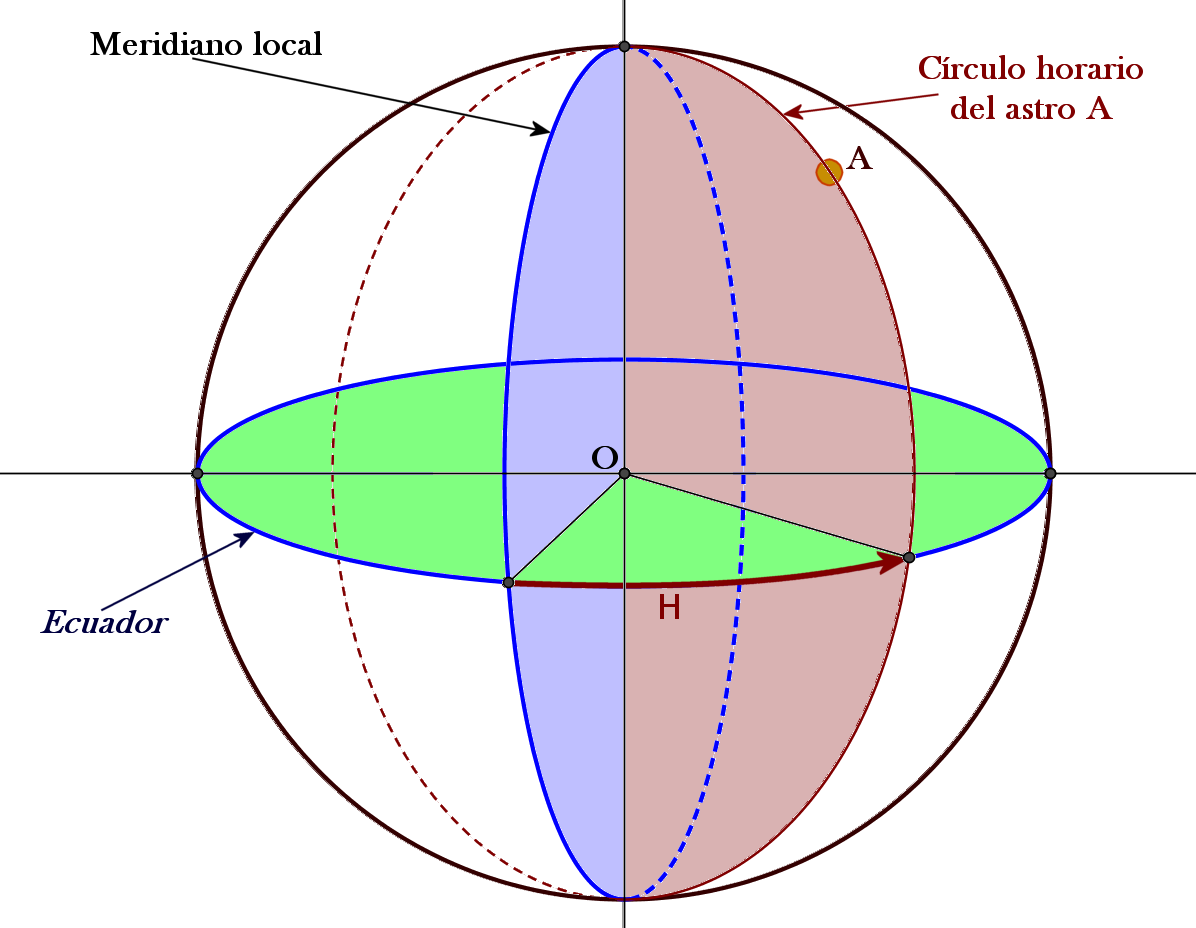
El ángulo horario es el arco de ecuador contado desde el punto de intersección del ecuador con el meridiano del observador hasta el círculo horario del astro, en sentido horario, el del movimiento aparente de la bóveda celeste.

INICIO REGRESAR

TIEMPO SIDERAL

El TIEMPO SIDERAL es el ángulo horario del punto vernal .

INICIO REGRESAR

COORDENADAS HORIZONTALES

REFERENCIAS

• CENTRO: Punto de obsdervación
• PLANO DE REFERENCIA: horizonte
• POLOS: cenit y nadir
• DIRECCIÓN PRINCIPAL: Puntos cardinales en el horizonte (SUR)

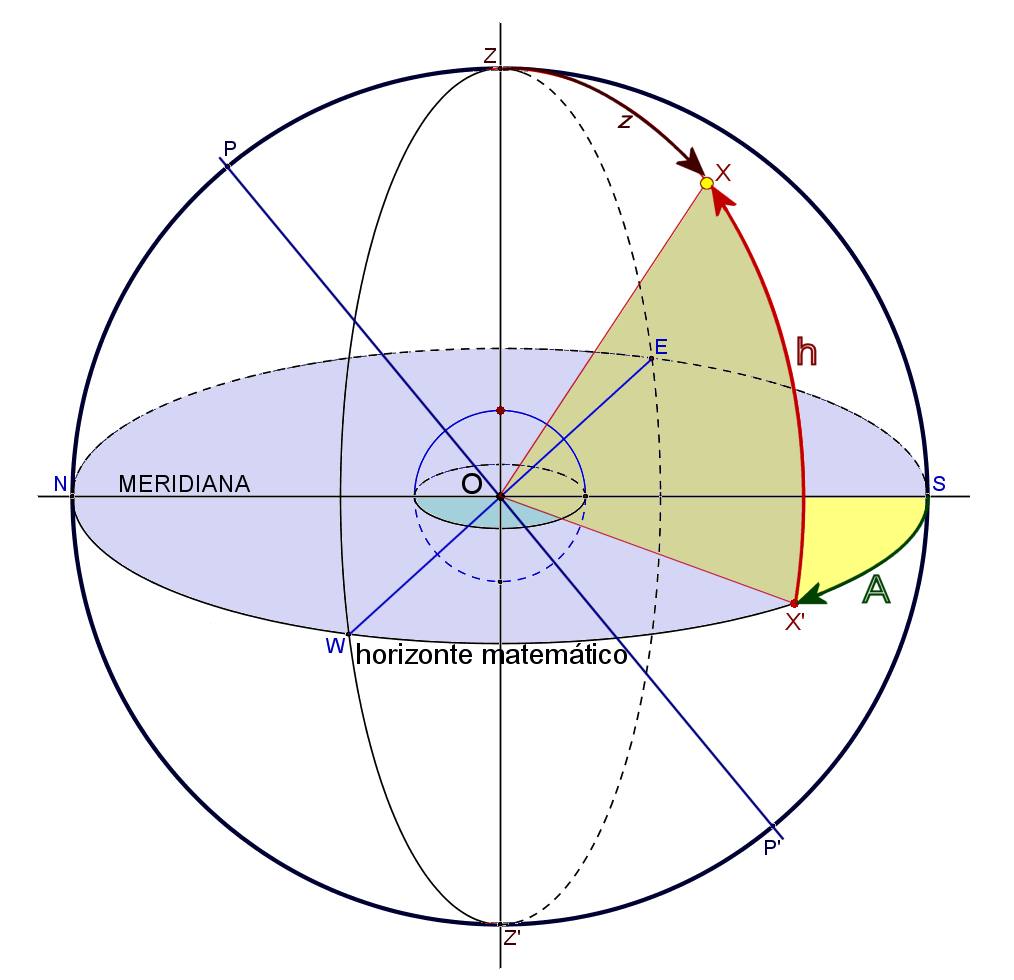
1. ZSZ'N ≡ Meridiano local
2. O ≡ Punto de observación
3. Z ≡ Cenit
4. Z' ≡ Nadir
5. P y P' ≡ Polos de la esfera celeste
6. PP' ≡ Eje del movimiento diurno
7. NS ≡ Meridiana

COORDENADAS

ALTURA SOBRE EL HORIZONTE, h

• Arco sobre el meridiano que pasa por el objeto desde el ecuador hacia el cenit o nadir.
• Se mide en GRADOS:
  • Positivo (0º y +90º) sobre el horizonte
  • Negativo (0º y -90º) bajo el horizonte

ACIMUT, A

• Arco sobre el ecuador medido entre el SUR y la proyección sobre el ECUADOR del objeto.
• Se mide en GRADOS:
  • Positivo (0º y 180º) en sentido horario (S-W-N)
  • Negativo (0º y -180) en sentido antihorario (S-E-N)

TRIEDRO (RECTANGULARES)

• EJE X: en la dirección de la meridiana, sentido creciente hacia el sur
• EJE Y: en la dirección de la perpendicular, sentido creciente hacia el oeste
• EJE Z: en la dirección de la vertical, sentido creciente hacia el cenit.

El triedro estará orientado en sentido retrógrado (giro de las agujas del reloj).

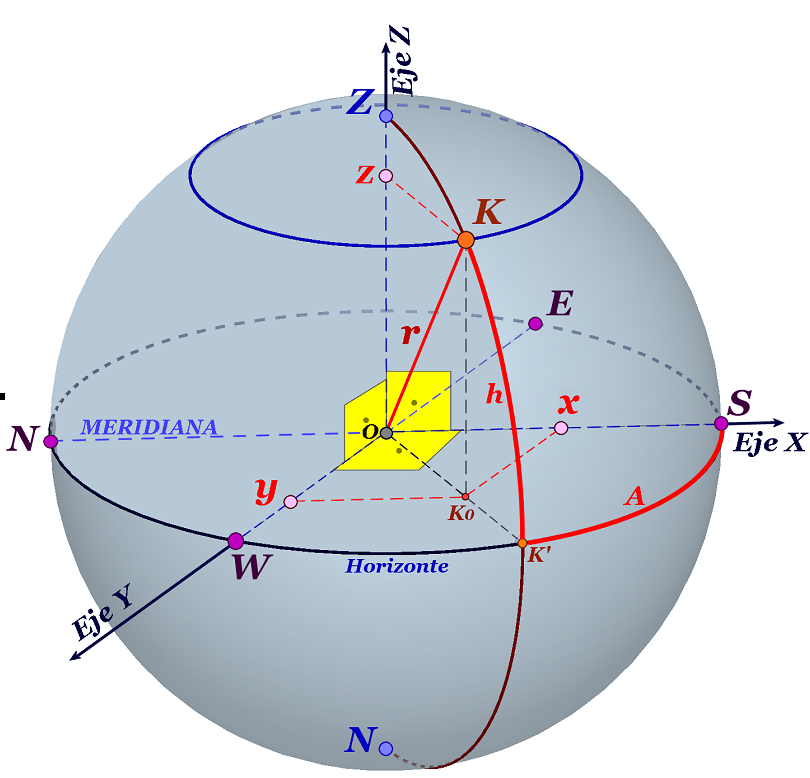
COORDENADAS CARTESIANAS (RECTANGULARES)

• El ángulo [SOK']=A
• el ángulo [KOK']=h

Con esto:

• $\left[O{K}_0\right]=r·cos\left(h\right)$
• $z=r·sen\left(h\right)$
• $x=\left[O{K}_0\right]·cos\left(A\right)$
• $y=\left[O{K}_0\right]·sen\left(A\right)$

Resumiendo:

$\{\begin{array}{c}x=r·cos\left(h\right)·cos\left(A\right)\\ y=r·cos\left(h\right)·sen\left(A\right)\\ z=r·sen\left(h\right)\end{array}$

INICIO REGRESAR

COORDENADAS HORARIAS

REFERENCIAS

• CENTRO: Punto de observación
• PLANO DE REFERENCIA: Ecuador celeste
• POLOS: Polos celestes
• DIRECCIÓN PRINCIPAL: Punto de aries

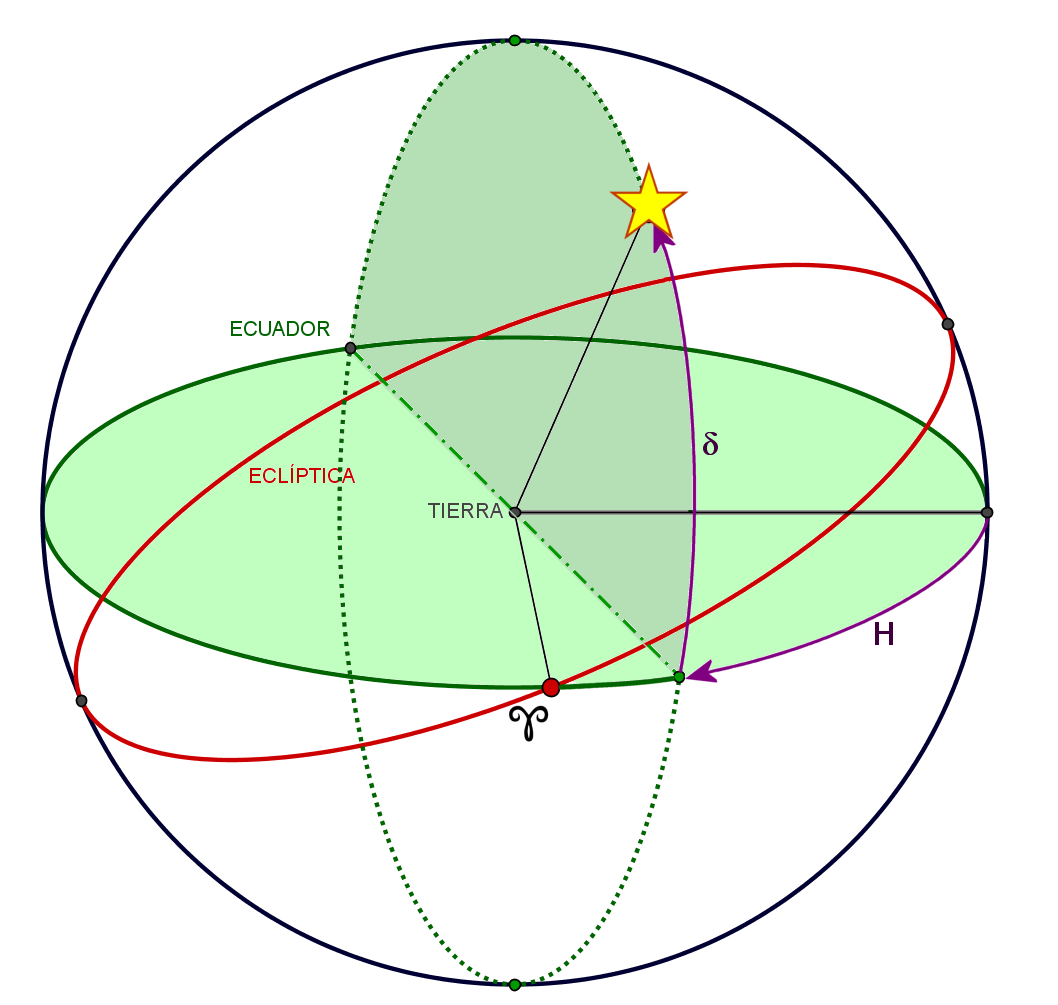
COORDENADAS

ÁNGULO HORARIO, H

• Ángulo que se forma en el ecuador entre el meridiano del observador y el círculo horario del objeto.
• Se mide en GRADOS:
  • Siempre positivo, Entre 0º y 360º
  • En sentido horario

DECLINACIÓN, δ

• Arco entre el punto de proyección del objeto sobre el ecuador y el objeto a lo largo de su meridiano.
• Se mide en GRADOS:
  • Positiva (0º y +90º) hacia el norte
  • Negativa (0º y -90º) hacia el sur

TRIEDRO (RECTANGULARES)

• EJE X': en la dirección de la línea del medio cielo, en sentido creciente hacia el medio cielo
• EJE Y': en la dirección de la perpendicular, en sentido creciente hacia el oeste
• EJE Z': en la dirección del eje del mundo, en sentido creciente hacia el polo norte

El triedro estará orientado en sentido retrógrado (giro de las agujas del reloj).

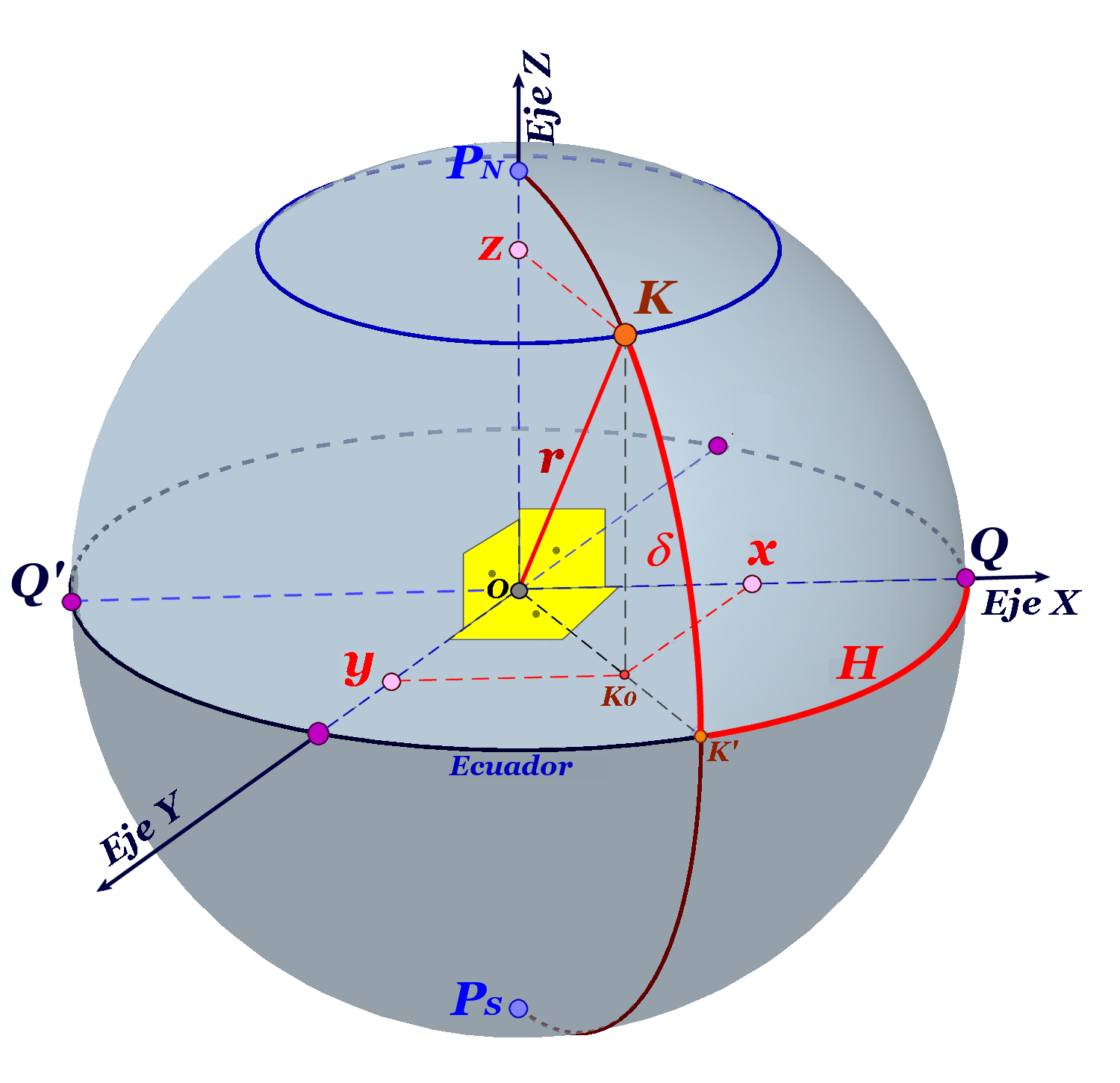
COORDENADAS CARTESIANAS (RECTANGULARES)

• El ángulo [QOK']=H
• el ángulo [KOK']=δ

Con esto:

• $\left[O{K}_0\right]=r·cos\left(\delta \right)$
• $z=r·sen\left(\delta \right)$
• $x=\left[O{K}_0\right]·cos\left(H\right)$
• $y=\left[O{K}_0\right]·sen\left(H\right)$

Resumiendo:

$\{\begin{array}{c}x=r·cos\left(\delta \right)·cos\left(H\right)\\ y=r·cos\left(\delta \right)·sen\left(H\right)\\ z=r·sen\left(\delta \right)\end{array}$

INICIO REGRESAR

COORDENADAS ECUATORIALES

REFERENCIAS

• CENTRO: Centro de la esfera celeste: La Tierra
• PLANO DE REFERENCIA: Ecuador celeste
• POLOS: Polos celestes
• DIRECCIÓN PRINCIPAL: Punto de aries

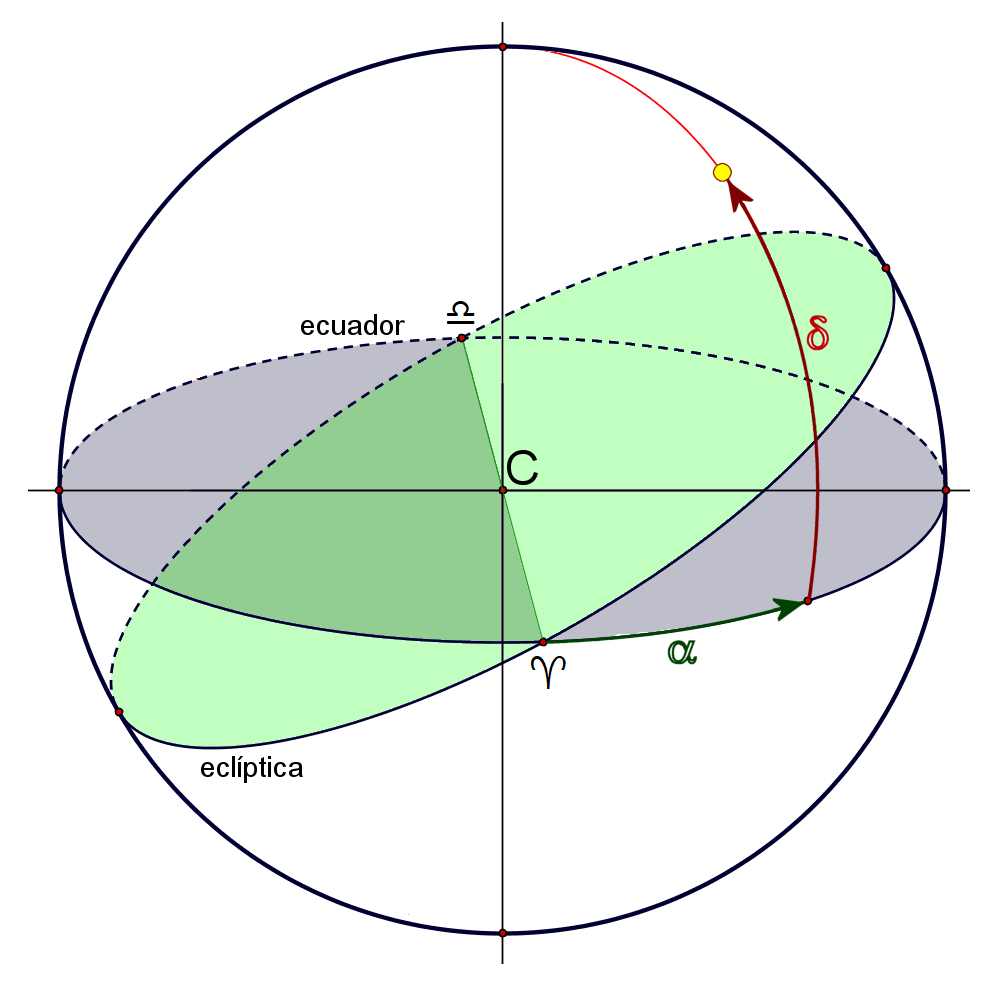
COORDENADAS

ASCENSIÓN RECTA, α

• Ángulo que se forma en el ecuador entre el meridiano del observador y el círculo horario del objeto.
• Se mide en ÁNGULOS HORARIOS:
  • Siempre positivo, Entre 0^h y 24^h
  • En sentido ANTIHORARIO

DECLINACIÓN, δ

• Arco entre el punto de proyección del objeto sobre el ecuador y el objeto a lo largo de su meridiano.
• Se mide en GRADOS:
  • Positiva (0º y +90º) hacia el norte
  • Negativa (0º y -90º) hacia el sur

TRIEDRO (RECTANGULARES)

• EJE X: Línea de equinoccios (semieje positivo)
• EJE Y: Sobre el Ecuador a 90º del eje X en sentido directo (antihorario)
• EJE Z: Dirección del Eje del mundo y positivo hacia el polo norte celeste

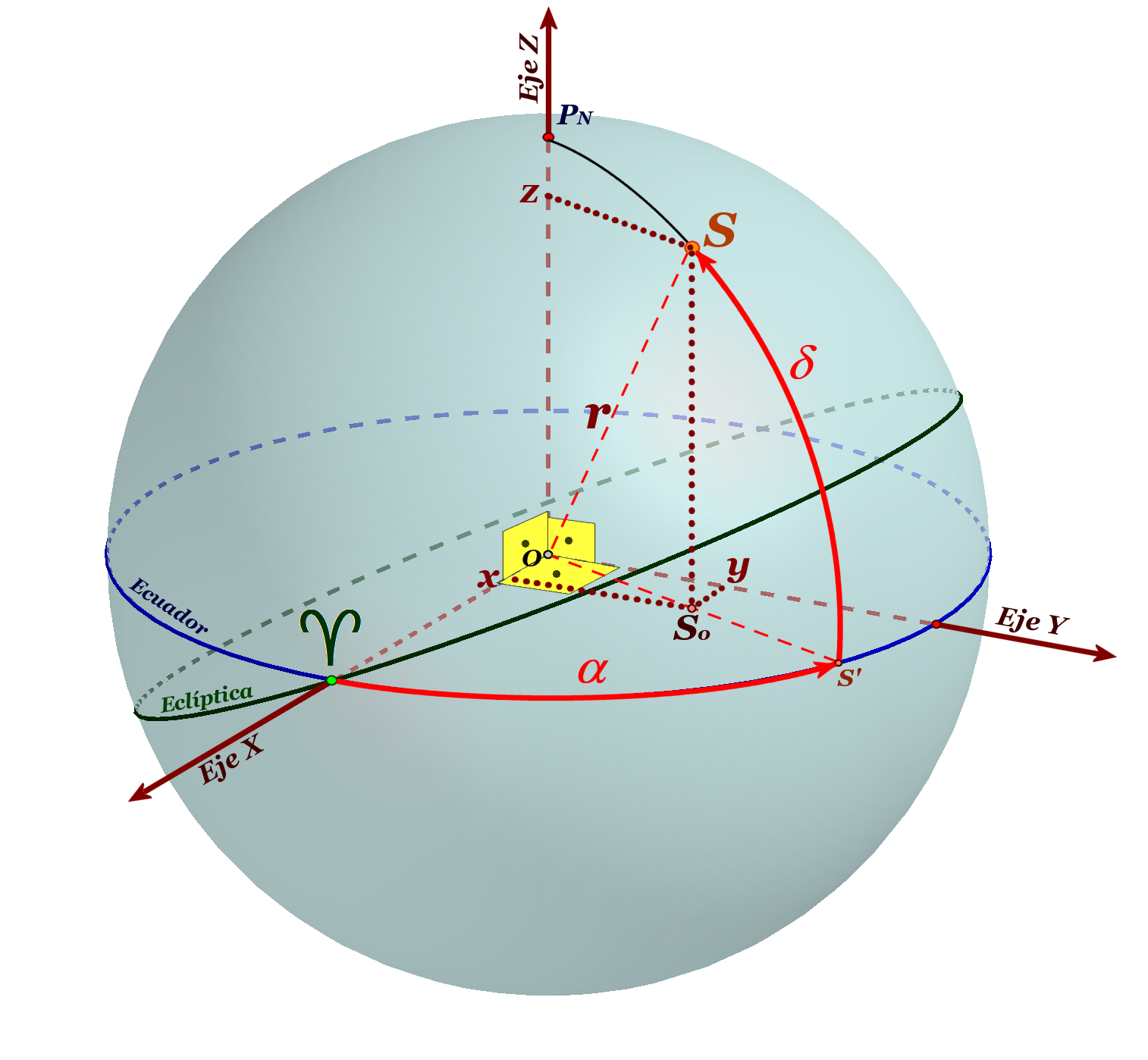
El triedro estará orientado en sentido directo (giro contrario al de las agujas del reloj).

COORDENADAS CARTESIANAS (RECTANGULARES)

• El ángulo [♈OS']=α
• el ángulo [SOS']=δ

Con esto:

• $\left[O{S}_0\right]=r·cos\left(\delta \right)$
• $z=r·sen\left(\delta \right)$
• $x=\left[O{S}_0\right]·cos\left(\alpha \right)$
• $y=\left[O{S}_0\right]·sen\left(\alpha \right)$

Resumiendo:

$\{\begin{array}{c}x=r·cos\left(\delta \right)·cos\left(\alpha \right)\\ y=r·cos\left(\delta \right)·sen\left(\alpha \right)\\ z=r·sen\left(\delta \right)\end{array}$

INICIO REGRESAR

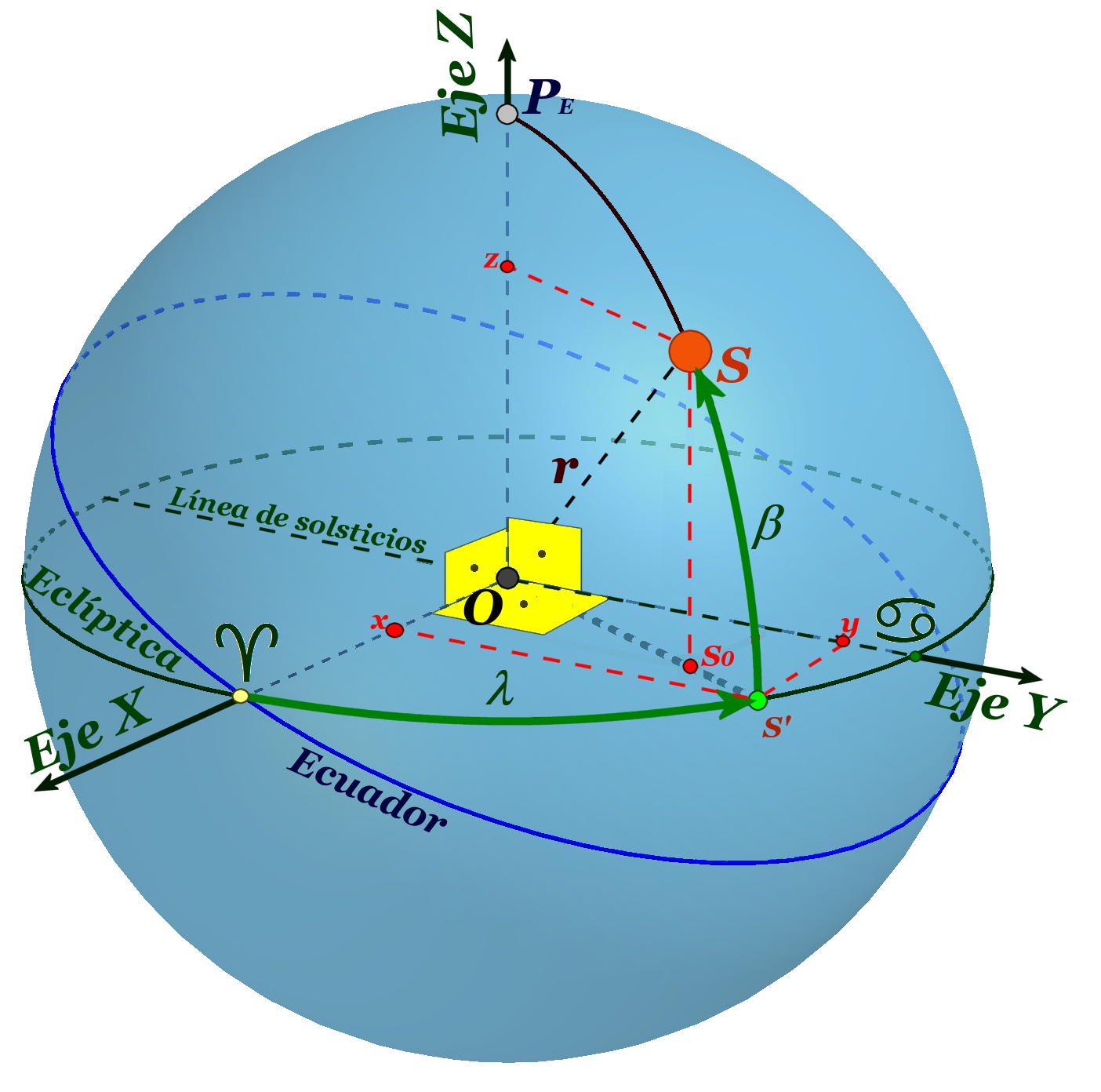
COORDENADAS ECLÍPTICAS

REFERENCIAS

• CENTRO: Centro de la esfera celeste: La Tierra
• PLANO DE REFERENCIA: Eclíptica
• POLOS: Polos eclípticos
• DIRECCIÓN PRINCIPAL: Punto de aries

COORDENADAS

LONGITUD CELESTE, L o λ

• Arco entre el punto de Aries y la proyección del objeto sobre la eclíptica.
• Se mide en GRADOS:
  • Siempre positivo (0º y 360º)
  • En sentido ANTIHORARIO

LATITUD CELESTE, B o β

• Arco que forma el objeto con el plano de la eclíptica.
• Se mide en GRADOS:
  • Positiva (0º y +90º) hacia el norte eclíptico
  • Negativa (0º y -90º) hacia el sur eclíptico

TRIEDRO (RECTANGULARES)

• EJE X: Línea de equinoccios (semieje positivo)
• EJE Y: Línea de solsticios a 90º del eje X en sentido directo (hacia Cancer)
• EJE Z: Dirección del eje de la eclíptica y positivo hacia el polo norte eclíptico

El triedro estará orientado en sentido directo (giro contrario al de las agujas del reloj).

COORDENADAS CARTESIANAS (RECTANGULARES)

• El ángulo [♈OS']=λ
• el ángulo [SOS']=β

Con esto:

• $\left[O{S}_0\right]=r·cos\left(\beta \right)$
• $z=r·sen\left(\lambda \right)$
• $x=\left[O{S}_0\right]·cos\left(\lambda \right)$
• $y=\left[O{S}_0\right]·sen\left(\lambda \right)$

Resumiendo:

$\{\begin{array}{c}x=r·cos\left(\beta \right)·cos\left(\lambda \right)\\ y=r·cos\left(\beta \right)·sen\left(\lambda \right)\\ z=r·sen\left(\beta \right)\end{array}$

INICIO REGRESAR

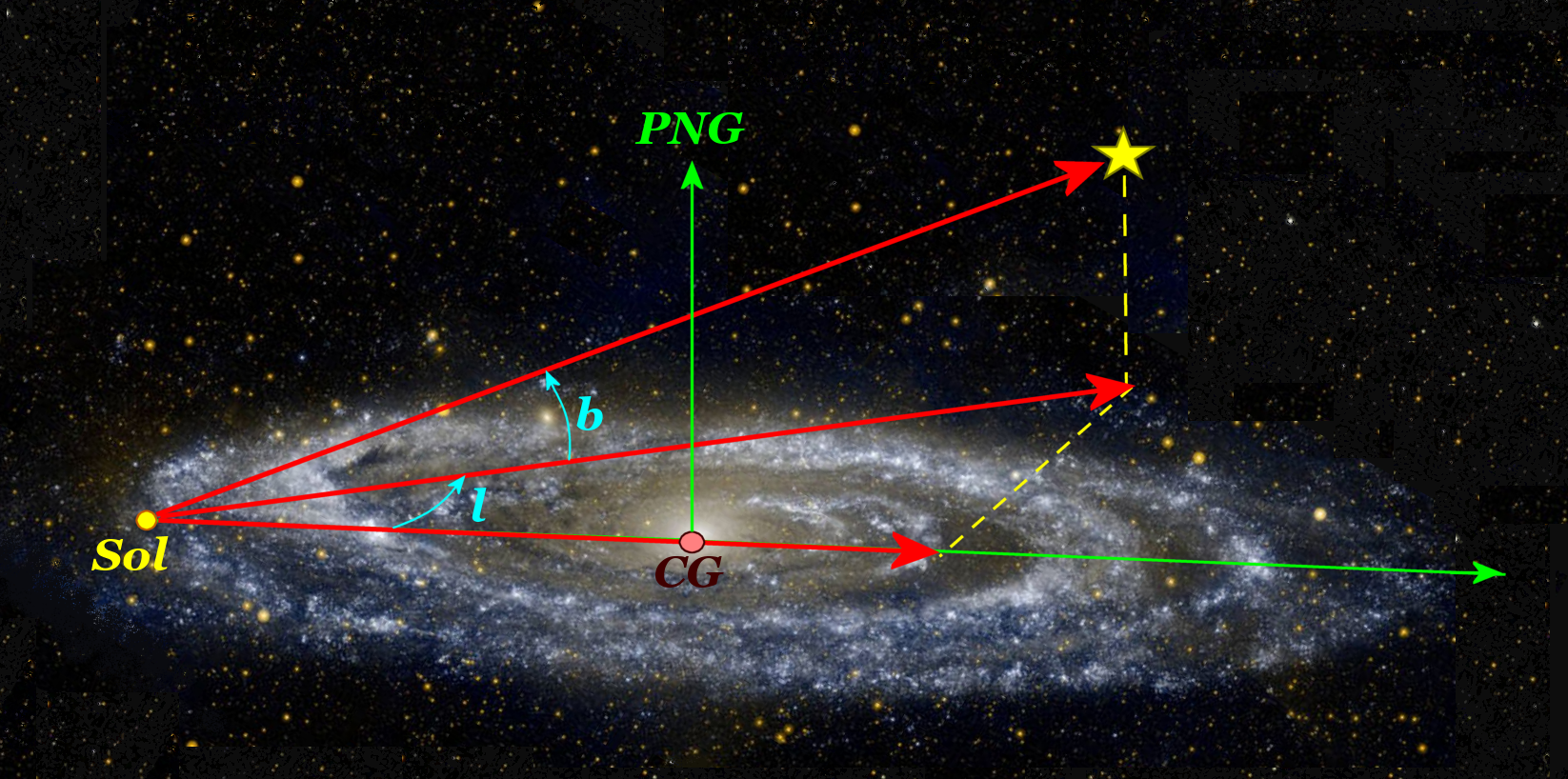
COORDENADAS GALÁCTICAS

REFERENCIAS

• CENTRO: El Sol
• PLANO DE REFERENCIA: Plano de la Galaxia
• POLOS: Polos galácticos
• DIRECCIÓN PRINCIPAL: Sol - Tierra

COORDENADAS

LONGITUD GALÁCTICA, l

• Es el ángulo que forma la dirección del Sol con el centro de la galaxia y la proyección del objeto sobre dicho plano.
• Se mide sobre el plano de la galaxia.
• Se mide en GRADOS:
  • Siempre positivo (0º y 360º)
  • Sentido antihorario desde el eje SOL-CENTRO GALAXIA

LATITUD GALÁCTICA, b

• Ángulo que forma el objeto con el plano de la galaxia.
• Se mide en GRADOS:
  • Positiva (0º y +90º) hacia el norte eclíptico
  • Negativa (0º y -90º) hacia el sur eclíptico

TRIEDRO

• EJE X: Apunta hacia el centro galáctico (l=0º y b=0º)
• EJE Y: Apunta hacia el sentido positivo del eje galáctico Y (l=90º y b=0º)
• EJE Z: Apunta hacia el polo norte galáctico (b=90º)

Se muestran los ejes galácticos (azul) superpuestos a los ecuatoriales (rojo).

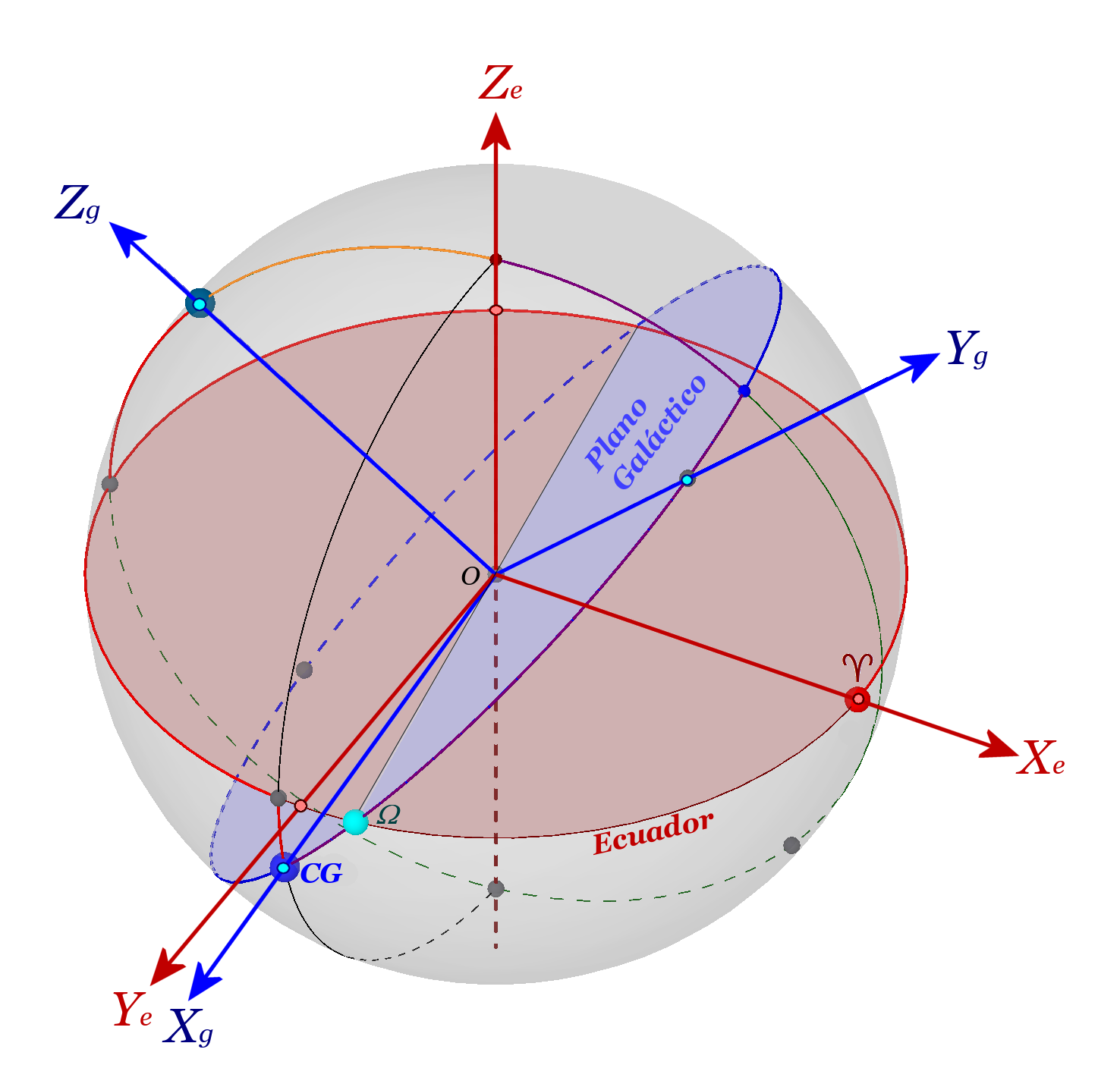
El triedro estará orientado en sentido directo (giro contrario al de las agujas del reloj).

INICIO REGRESAR

CONVERSIÓN HORARIAS - HORIZONTALES

Los triedros de referencia de los sistemas de coordenadas horizontales y horarias tienen el eje Y común y ambos están orientados en sentido retrógrado, por lo que podrá efectuarse el cambio de un sistema al otro por un simple giro alrededor del eje Y≡Y', de ángulo (90º-φ), siendo φ la latitud del punto de observación.

De HORARIAS A HORIZONTALES

1. Partimos de las coordenadas horarias (δ,H)
2. Convertir de coordenadas esféricas a coordenadas cartesianas $\{\begin{array}{c}x\text{'}=cos\left(\delta \right)·cos\left(H\right)\\ y\text{'}=cos\left(\delta \right)·sen\left(H\right)\\ z\text{'}=sen\left(\delta \right)\end{array}$
3. Efectuar rotación R_Y(90-φ) ⇒ $\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\begin{array}{c} \\ R_Y(\mathrm{90}-\phi )\\ \end{array}·\left(\begin{array}{c}x\text{'}\\ y\text{'}\\ z\text{'}\end{array}\right)$

   Rotación: $R_Y(\mathrm{90}-\phi )=\left(\begin{array}{ccc}cos(\mathrm{90}-\phi )& 0& sen(\mathrm{90}-\phi )\\ 0& 1& 0\\ -sen(\mathrm{90}-\phi )& 0& cos(\mathrm{90}-\phi )\end{array}\right)=\left(\begin{array}{ccc}sen\left(\phi \right)& 0& cos\left(\phi \right)\\ 0& 1& 0\\ -cos\left(\phi \right)& 0& sen\left(\phi \right)\end{array}\right)$

4. Convertir de coordenadas cartesianas a coordenadas esféricas $\{\begin{array}{c}x=cos\left(h\right)·cos\left(A\right)\\ y=cos\left(h\right)·sen\left(A\right)\\ z=sen\left(h\right)\end{array}$

   Despejando:

   $h=\text{arc sen}\left(z\right)$

   $A=\text{arc tan}\left(\frac{y}{x}\right)$

De HORIZONTALES A HORARIAS

1. Partimos de las coordenadas horizontales (A,h)
2. Convertir de coordenadas esféricas a coordenadas cartesianas $\{\begin{array}{c}x=cos\left(h\right)·cos\left(A\right)\\ y=cos\left(h\right)·sen\left(A\right)\\ z=sen\left(h\right)\end{array}$
3. Efectuar rotación R_Y(φ-90) ⇒ $\left(\begin{array}{c}x\text{'}\\ y\text{'}\\ z\text{'}\end{array}\right)=\begin{array}{c} \\ R_Y(\phi -\mathrm{90})\\ \end{array}·\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$

   Rotación: $R_Y(\phi -\mathrm{90})=\left(\begin{array}{ccc}cos(\phi -\mathrm{90})& 0& sen(\phi -\mathrm{90})\\ 0& 1& 0\\ -sen(\phi -\mathrm{90})& 0& cos(\phi -\mathrm{90})\end{array}\right)=\left(\begin{array}{ccc}cos(-(\mathrm{90}-\phi \left)\right)& 0& sen(-(\mathrm{90}-\phi \left)\right)\\ 0& 1& 0\\ -sen(-(\mathrm{90}-\phi \left)\right)& 0& cos(-(\mathrm{90}-\phi \left)\right)\end{array}\right)=\left(\begin{array}{ccc}cos(\mathrm{90}-\phi )& 0& -sen(\mathrm{90}-\phi )\\ 0& 1& 0\\ sen(\mathrm{90}-\phi )& 0& cos(\mathrm{90}-\phi )\end{array}\right)=\left(\begin{array}{ccc}sen\left(\phi \right)& 0& -cos\left(\phi \right)\\ 0& 1& 0\\ cos\left(\phi \right)& 0& sen\left(\phi \right)\end{array}\right)$

4. Convertir de coordenadas cartesianas a coordenadas esféricas $\{\begin{array}{c}x\text{'}=cos\left(\delta \right)·cos\left(H\right)\\ y\text{'}=cos\left(\delta \right)·sen\left(H\right)\\ z\text{'}=sen\left(\delta \right)\end{array}$

   Despejando:

   $\delta =\text{arc sen}\left(z\text{'}\right)$

   $H=\text{arc tan}\left(\frac{y\text{'}}{x\text{'}}\right)$

ACLARACIÓN

Para cualquier ángulo dado η la matriz R_Y(η) es ortonormal, es decir:

• |R_Y(η)| = 1
• R_Y(η)^-1 = R_Y(η)^T

Como la matriz R_Y(90-φ) es ortonormal, se cumple que:

${R_Y(\mathrm{90}-\phi )}^{\mathrm{-1}}={R_Y(\mathrm{90}-\phi )}^T=R_Y(\phi -\mathrm{90})$

Así pues, si $\begin{array}{c} \\ V\\ \end{array}=\begin{array}{c} \\ R_Y(\mathrm{90}-\phi )\\ \end{array}·\begin{array}{c} \\ V\text{'}\\ \end{array}$ entonces $\begin{array}{c} \\ V\text{'}\\ \end{array}=\begin{array}{c} \\ {R_Y(\mathrm{90}-\phi )}^{-1}\\ \end{array}·\begin{array}{c} \\ V\\ \end{array}=\begin{array}{c} \\ {R_Y(\mathrm{90}-\phi )}^T\\ \end{array}·\begin{array}{c} \\ V\\ \end{array}=\begin{array}{c} \\ R_Y(\phi -\mathrm{90})\\ \end{array}·\begin{array}{c} \\ V\\ \end{array}$

INICIO REGRESAR

CONVERSIÓN ECUATORIALES - ECLIPTICAS

Los triedros de referencia de los sistemas de coordenadas ecuatoriales y eclípticas tienen común el eje X, y ambos están orientados en sentido directo, por lo que podrá efectuarse el cambio de un sistema al otro por una simple rotación R_X alrededor del eje X de ángulo ε.

De ECUATORIALES A ECLÍPTICAS

1. Partimos de las coordenadas ecuatoriales (α,δ)
2. Convertir de coordenadas esféricas a coordenadas cartesianas $\{\begin{array}{c}x=cos\left(\delta \right)·cos\left(\alpha \right)\\ y=cos\left(\delta \right)·sen\left(\alpha \right)\\ z=sen\left(\delta \right)\end{array}$
3. Efectuar rotación R_X(ε) ⇒ $\left(\begin{array}{c}x\text{'}\\ y\text{'}\\ z\text{'}\end{array}\right)=\begin{array}{c} \\ R_X\left(\epsilon \right)\\ \end{array}·\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$

   Rotación: $R_X\left(\epsilon \right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\left(\epsilon \right)& -sen\left(\epsilon \right)\\ 0& sen\left(\epsilon \right)& cos\left(\epsilon \right)\end{array}\right)$

4. Convertir de coordenadas cartesianas a coordenadas esféricas $\{\begin{array}{c}x\text{'}=cos\left(\beta \right)·cos\left(\lambda \right)\\ y\text{'}=cos\left(\beta \right)·sen\left(\lambda \right)\\ z\text{'}=sen\left(\beta \right)\end{array}$

   Despejando:

   $\beta =\text{arc sen}\left(z\text{'}\right)$

   $\lambda =\text{arc tan}\left(\frac{y\text{'}}{x\text{'}}\right)$

De ECLÍPTICAS A ECUATORIALES

1. Partimos de las coordenadas eclípticas (λ,β)
2. Convertir de coordenadas esféricas a coordenadas cartesianas $\{\begin{array}{c}x\text{'}=cos\left(\beta \right)·cos\left(\lambda \right)\\ y\text{'}=cos\left(\beta \right)·sen\left(\lambda \right)\\ z\text{'}=sen\left(\beta \right)\end{array}$
3. Efectuar rotación R_X(-ε) ⇒ $\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\begin{array}{c} \\ R_X(-\epsilon )\\ \end{array}·\left(\begin{array}{c}x\text{'}\\ y\text{'}\\ z\text{'}\end{array}\right)$

   Rotación: $R_X(-\epsilon )=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos(-\epsilon )& -sen(-\epsilon )\\ 0& sen(-\epsilon )& cos(-\epsilon )\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\left(\epsilon \right)& sen\left(\epsilon \right)\\ 0& -sen\left(\epsilon \right)& cos\left(\epsilon \right)\end{array}\right)$

4. Convertir de coordenadas cartesianas a coordenadas esféricas $\{\begin{array}{c}x=cos\left(\delta \right)·cos\left(\alpha \right)\\ y=cos\left(\delta \right)·sen\left(\alpha \right)\\ z=sen\left(\delta \right)\end{array}$

   Despejando:

   $\delta =\text{arc sen}\left(z\right)$

   $\alpha =\text{arc tan}\left(\frac{y}{x}\right)$

ACLARACIÓN

Para cualquier ángulo dado η la matriz R_Y(η) es ortonormal, es decir:

• |R_Y(η)| = 1
• R_Y(η)^-1 = R_Y(η)^T

Como la matriz R_X(-ε) es ortonormal, se cumple que:

${R_X(-\epsilon )}^{\mathrm{-1}}={R_X(-\epsilon )}^T=R_X\left(\epsilon \right)$

Así pues, si $\begin{array}{c} \\ V\text{'}\\ \end{array}=\begin{array}{c} \\ R_X\left(\epsilon \right)\\ \end{array}·\begin{array}{c} \\ V\\ \end{array}$ entonces $\begin{array}{c} \\ V\\ \end{array}=\begin{array}{c} \\ {R_X\left(\epsilon \right)}^{-1}\\ \end{array}·\begin{array}{c} \\ V\text{'}\\ \end{array}=\begin{array}{c} \\ {R_X\left(\epsilon \right)}^T\\ \end{array}·\begin{array}{c} \\ V\\ \end{array}=\begin{array}{c} \\ R_X(-\epsilon )\\ \end{array}·\begin{array}{c} \\ V\\ \end{array}$

INICIO REGRESAR