DESCRIPCIÓN DEL PROBLEMA

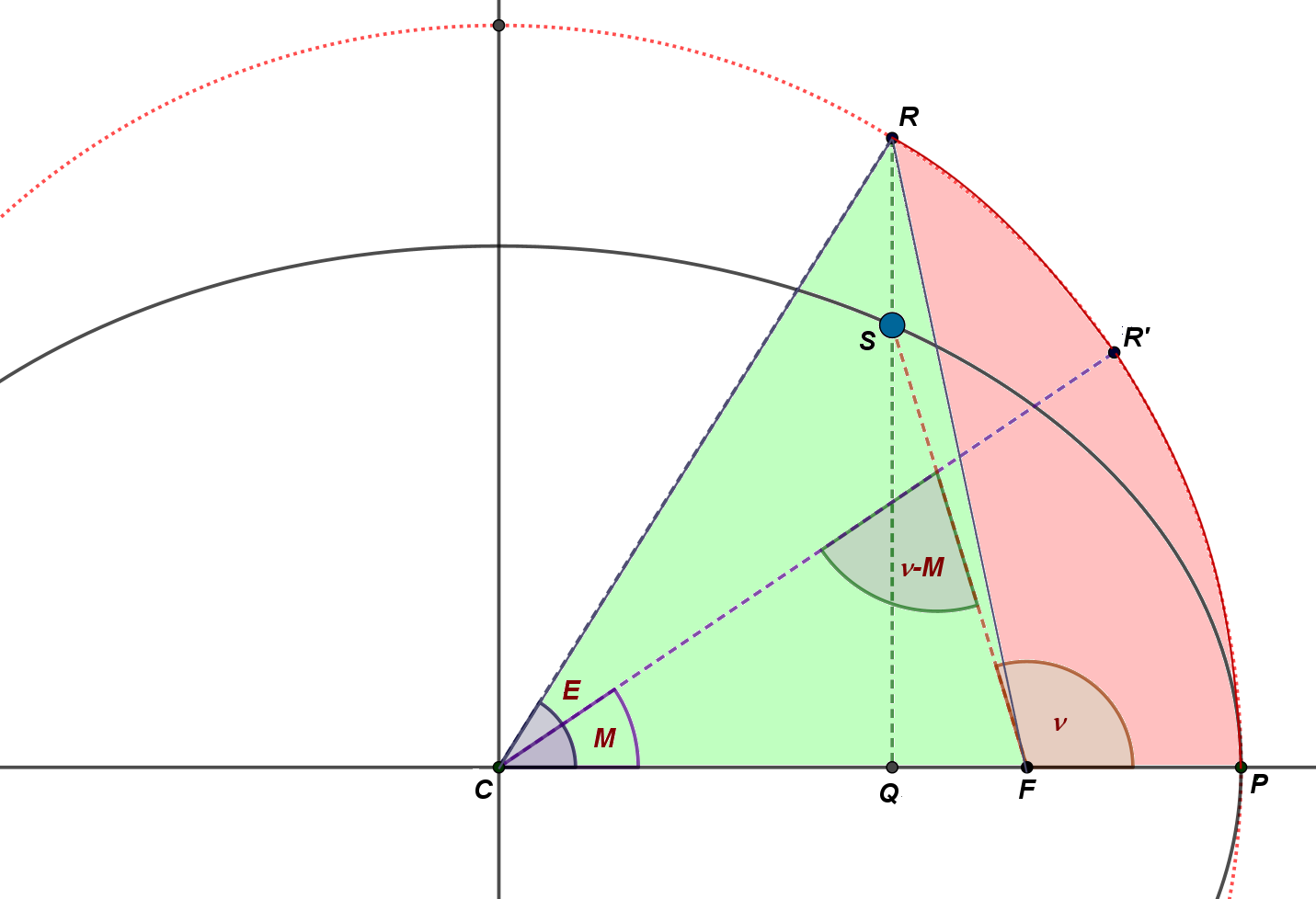
Consideremos la órbita elíptica de un planeta S:

1. Elipse con centro en C y focos en F y F'.
2. Circunferencia principal con centro en C y radio a.
3. El sol se encuentra en el foco F .
4. Semiejes mayor y menor a y b respectivamente.
5. Semidistancia focal, c.
6. Afelio y Perihelio A y P respectivamente.
7. Consideremos un instante de tiempo inicial t₀ coincidente con el paso por el perihelio P, y un instante de tiempo arbitrario t con el paso del planeta por el punto S.
   El tiempo transcurrido entre P y S es: $T=t-t_0$
8. Sea τ en tiempo empleado en completar todo un giro de órbita, comenzando en el perihelio.

Supongamos un planeta que comienza a girar en su órbita desde el Perihelio. Este movimiento no es uniforme (2ª ley de Kepler), por lo que supondremos un planeta ficticio que gira a la vez pero siguiendo una órbita circular (circunferencia principal) con movimiento uniforme.

Cuando el planeta REAL está en S (con movimiento no uniforme, más rápido cerca del perihelio y más lento por el afelio), el FICTICIO irá más retrasado (o adelantado), encontrándose en la posición R'

Trazando una perpendicular al eje mayor de la elipse por el punto S ,cortará a la circunferencia principal en el punto R

ANOMALÍAS

Media, M.

Es el ángulo PCR'

Excéntrica, E.

Es el ángulo PCR

Verdadera, ν.

Es el ángulo PFR

ECUACIÓN DEL CENTRO, ν-M.

Es el ángulo que se forma entre CR' y FS

INICIO REGRESAR

ECUACIÓN DE KEPLER

1. El movimiento medio, n es el ángulo recorrido por unidad de tiempo en un movimiento uniforme: $\left.\begin{array}{ccc}\text{TIEMPOS}& & \text{ÁNGULOS}\\ \tau & \to & 2·\pi \\ 1& \to & n\end{array}\right\}\Rightarrow n=\frac{2·\pi }{\tau }$
2. La anomalía media, M es: $M=n·(t-t_0)=\frac{2·\pi }{\tau }·T$
3. Consideremos τ como UNIDAD, el tiempo T será una fracción de τ: $\frac{T}{\tau }$
4. Consideremos un giro completo como UNIDAD, el ángulo E será una fracción de 2π: $\frac{E}{2·\pi }$
5. Área del sector del círculo barrido según el ángulo E, S_PCR
   $\left.\begin{array}{ccc}\text{Tiempos}& & \text{Áreas}\\ 1& \to & \pi ·a^2\\ \frac{E}{2·\pi }& \to & S_{\mathrm{PCR}}\end{array}\right\}\Rightarrow S_{\mathrm{PCR}}=a^2·\pi ·\frac{E}{2·\pi }=\frac{a^2}{2}·E$
6. Área del sector del círculo S_PFR y el área del sector de elipse S_PFS son homólogas, por lo que cumplen con la relación de áreas
   $S_{\mathrm{PFR}}=\frac{a}{b}·S_{\mathrm{PFS}}$
7. Área del sector de la elipse S_PFS barrido en el tiempo T
   $\left.\begin{array}{ccc}\text{Tiempos}& & \text{Áreas}\\ 1& \to & \pi ·a·b\\ \frac{T}{\tau }& \to & S_{\mathrm{PFS}}\end{array}\right\}\Rightarrow S_{\mathrm{PFS}}=\pi ·a·b·\frac{T}{\tau }$
8. Sustituimos estas dos expresiones (6ª y 7ª)
   $S_{\mathrm{PFR}}=\frac{a}{b}·S_{\mathrm{PFS}}=\frac{a}{b}·\frac{T}{\tau }·\pi ·a·b=\pi ·a^2·\frac{T}{\tau }$
9. Área del triángulo S_FCR
   $S_{\mathrm{FCR}}=\frac{1}{2}·c·(a·sen(E\left)\right)=\frac{1}{2}·a·e·a·sen\left(E\right)=\frac{1}{2}·a^2·e·sen\left(E\right)$
10. Área del sector circular S_PCR. Cálculo directo
    $S_{\mathrm{PCR}}=S_{\mathrm{PFR}}+S_{\mathrm{FCR}}\Rightarrow S_{\mathrm{PFR}}=S_{\mathrm{PCR}}-S_{\mathrm{FCR}}$
11. Sustituyendo cada término por su expresión (de izquierda a derecha, 8ª, 5ª y 9ª)
    $[\pi ·a^2·\frac{T}{\tau }]=[\frac{a^2}{2}·E]-[\frac{1}{2}·a^2·e·sen(E\left)\right]$
12. Agrupamos, transponemos y simplificamos
    $2·\pi ·\frac{T}{\tau }=E-e·sen\left(E\right)$
13. Expresamos el primer miembro como la anomalía media (2ª)
    

INICIO REGRESAR

ELEMENTOS ORBITALES

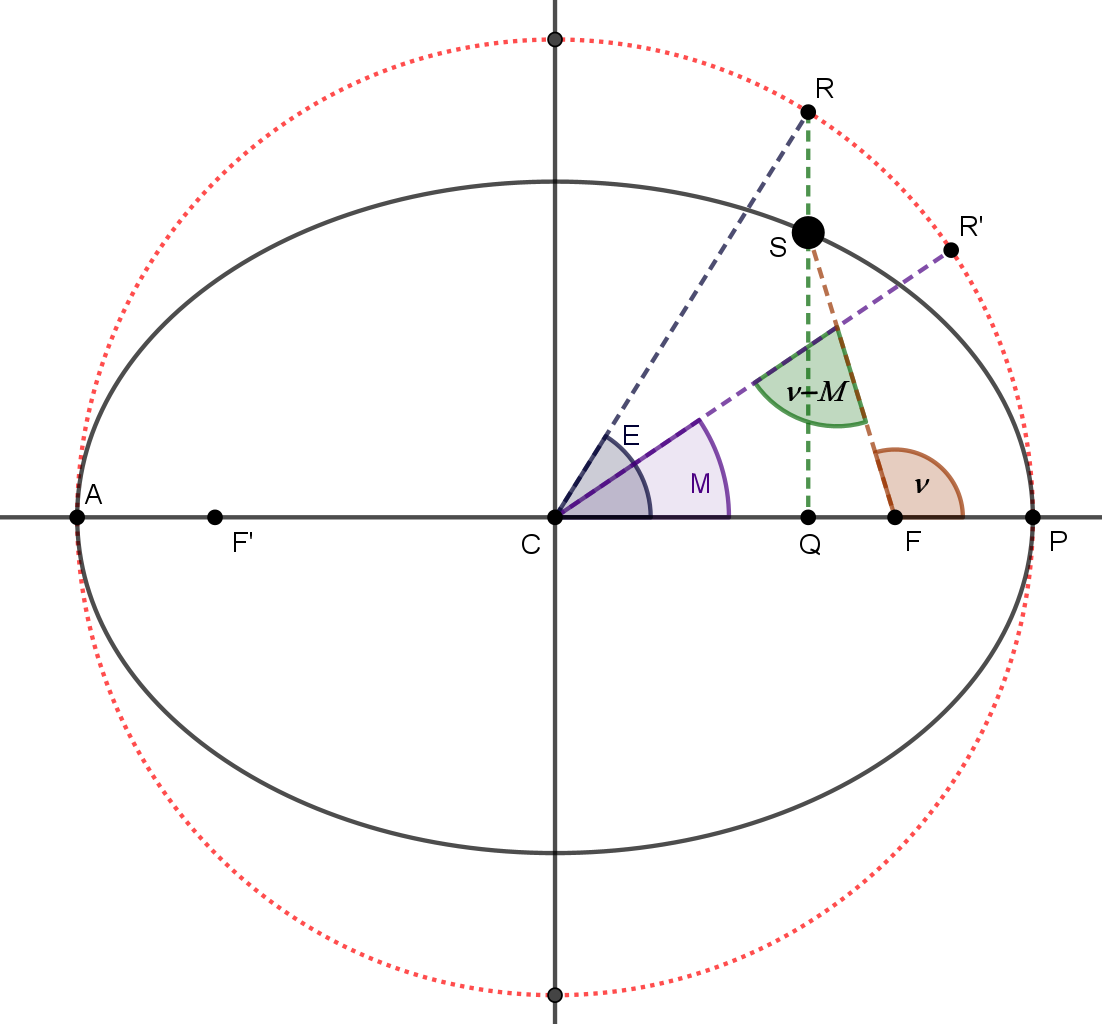
Son todos los parámetros necesarios para identificar unívocamente la órbita de un planeta.

Son llamados elementos keplerianos, y son los siguientes:

ELEMENTOS KEPLERIANOS

• SEMIEJE MAYOR DE LA ÓRBITA
  • Es la distancia d(C,A)=d(C,P).
  • Se representa por la letra a.
  • Se mide en UA.
• EXCENTRICIDAD DE LA ÓRBITA
  • Es un valor absoluto entre 0 y 1. Cuando vale 0, la elipse se transforma en circunferencia.
  • Se representa por la letra e.
• INCLINACIÓN DE LA ÓRBITA
  • Es un valor angular que indica cuánto está inclinada con respecto a la eclíptica.
  • Se representa por la letra i.
• LONGITUD DEL NODO ASCENDENTE
  • Indica el ángulo medido desde el punto vernal en el momento que la órbita atraviesa la eclíptica.
  • Se representa por la letra Ω.
• ARGUMENTO DEL PERIHELIO
  • Indica el ángulo comprendido entre el nodo ascendente y el perihelio. Determina la orientación de la órbita.
  • Se representa por la letra ω.
• ANOMALÍA MEDIA
  • Es el ángulo determinado por la proyección del planeta sobre la circunferencia principal y el semieje mayor.
  • Se representa por la letra M.

OTROS ELEMENTOS

• ANOMALÍA EXCÉNTRICA
  • Es el ángulo medido desde el centro de la elipse, que forma la proyección R del planeta sobre la circunferencia principal, y el eje de la elipse.
  • Se representa por la letra E.
• ANOMALÍA VERDADERA
  • Es el ángulo que forman las líneas foco-planeta y foco-perihelio.
  • Se representa por la letra ν.
• ECUACIÓN DEL CENTRO
  • Es la diferencia angular entre la posición real del planeta en órbita elíptica (con movimiento no uniforme) y la posición ficticia en órbita circular (con movimiento uniforme).
  • La ecuación es ν - M.
• LONGITUD MEDIA DEL PLANETA
  • Es una de las coordenadas eclípticas medida sobre el ecuador medio
  • Se representa por la letra L.

INICIO REGRESAR